期权定价是金融领域一个复杂而重要的课题。其中，二叉树模型作为一种简单直观的数值方法，被广泛应用于期权定价，尤其是在教学和理解期权定价原理方面。二叉树模型通过模拟标的资产价格在离散时间点上的可能路径，来计算期权的理论价值。将深入探讨期权二叉树计算公式，并详细解释多期二叉树的坐标系统，帮助读者理解和应用这一模型。

二叉树模型的基本原理

二叉树模型的核心思想是将标的资产价格的变动离散化为一系列的上下波动。假设当前标的资产价格为S，在下一个时间点，价格可能上涨到uS，也可能下跌到dS，其中u > 1，d < 1。模型通过构建一个二叉树，模拟标的资产价格在不同时间点的所有可能路径。每个节点代表一个特定的时间点和标的资产价格，而连接节点的边则代表价格上涨或下跌的概率。通过回溯法，从期权到期日的价值开始，逐步计算每个节点上的期权价值，最终得到当前时间点的期权理论价值。

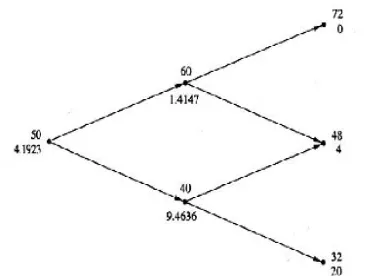
二叉树模型的关键参数包括：

• 标的资产价格(S): 当前标的资产的市场价格。
• 执行价格(K): 期权合约规定的买入或卖出标的资产的价格。
• 到期时间(T): 期权合约到期的时间。
• 无风险利率(r): 无风险资产的利率。
• 波动率(σ): 标的资产价格的波动程度。
• 上涨因子(u): 标的资产价格上涨的比例。
• 下跌因子(d): 标的资产价格下跌的比例。
• 风险中性概率(p): 在风险中性世界中，标的资产价格上涨的概率。

期权二叉树计算公式

期权二叉树模型的计算公式主要分为两个步骤：前向构建二叉树和后向计算期权价值。

1. 前向构建二叉树：

需要确定二叉树的层数n，这取决于将到期时间T划分为多少个时间段。每个时间段的长度为Δt = T/n。计算上涨因子u和下跌因子d。常用的计算方法包括：

• Cox-Ross-Rubinstein (CRR) 模型： u = exp(σ√Δt), d = 1/u
• Jarrow-Rudd 模型： u = exp((r - 0.5σ²)Δt + σ√Δt), d = exp((r - 0.5σ²)Δt - σ√Δt)

计算风险中性概率p：

p = (exp(rΔt) - d) / (u - d)

根据S、u、d和n，构建二叉树。每个节点(i, j)代表第i个时间段，标的资产价格经过j次上涨后的价格，其中i = 0, 1, ..., n，j = 0, 1, ..., i。节点(i, j)的标的资产价格为：

S_i,j = S u^j d^(i-j)

2. 后向计算期权价值：

从二叉树的最后一层（到期日）开始，计算每个节点的期权价值。对于欧式看涨期权，到期日的期权价值为：

C_n,j = max(S_n,j - K, 0)

对于欧式看跌期权，到期日的期权价值为：

P_n,j = max(K - S_n,j, 0)

从后向前，逐步计算每个节点的期权价值。对于节点(i, j)，其期权价值为：

C_i,j = exp(-rΔt) (p C_i+1,j+1 + (1-p) C_i+1,j)

P_i,j = exp(-rΔt) (p P_i+1,j+1 + (1-p) P_i+1,j)

最终，节点(0, 0)的期权价值即为当前时间点的期权理论价值。

多期二叉树坐标系统

在多期二叉树中，每个节点都需要一个坐标来唯一标识其位置。常用的坐标系统是 (i, j)，其中 i 代表时间步数（从0到n），j 代表从初始节点到该节点的价格上涨次数（从0到i）。节点 (0, 0) 代表初始状态，节点 (n, j) 代表到期日，价格上涨了 j 次。 理解这个坐标系统对于理解和实现二叉树模型至关重要。

例如，在一个3期二叉树中，节点 (2, 1) 代表经过两个时间步，价格上涨了一次。这意味着标的资产价格经历了以下路径之一：

• 上涨 -> 下跌
• 下跌 -> 上涨

节点 (3, 3) 代表经过三个时间步，价格全部上涨。节点 (3, 0) 代表经过三个时间步，价格全部下跌。

二叉树模型的优缺点

优点：

• 简单直观，易于理解和实现。
• 可以处理美式期权，通过在每个节点比较持有期权和立即执行期权的价值，来确定最优执行策略。
• 可以灵活地调整模型参数，以适应不同的市场情况。

缺点：

• 计算量随着期数的增加而呈指数增长，可能导致计算效率低下。
• 对波动率的估计较为敏感，波动率的微小变化可能导致期权价值的显著差异。
• 离散化处理可能导致定价误差，需要增加期数来提高精度。

二叉树模型的应用

二叉树模型不仅可以用于期权定价，还可以应用于其他金融衍生品的定价，例如可转换债券、奇异期权等。二叉树模型还可以用于投资组合管理、风险管理等领域。例如，可以通过构建多个二叉树，模拟不同资产价格的变动，来评估投资组合的风险收益特征。

期权二叉树模型是一种简单而强大的期权定价工具。通过理解其基本原理、计算公式和坐标系统，可以更好地理解期权定价的内在逻辑，并将其应用于实际的金融决策中。虽然二叉树模型存在一些局限性，但它仍然是金融领域不可或缺的工具之一，尤其是在教学和理解期权定价原理方面。 随着计算机技术的不断发展，更复杂的数值方法，例如蒙特卡洛模拟，也得到了广泛应用。二叉树模型作为理解期权定价的基石，仍然具有重要的价值。